Matematika

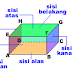
BALOK
 
Definisi Balok

Balok adalah suatu bangun ruang yang dibatasi oleh 6 persegi panjang , di mana setiap sisi persegipanjang berimpit dengan tepat satu sisi persegipanjang yang lain dan persegipanjang yang sehadap adalah kongruen.

Terdapat 6 buah sisi yang berbentuk persegipanjang yang membentuk balok posisinya adalah :

sisi alas sisi depan sisi atas sisi belakang sisi kiri sisi kanan

sisi alas kongruen dengan sisi atas
sisi depan kongruen dengan sisi belakang
sisi kiri kongruen dengan sisi kanan

Penamaan balok disesuaikan dengan nama sisi alas dan sisi atas.

Jika sisi alas balok adalah ABCD, dan sisi atas balok adalah EFGH, maka balok tersebut dinamakan balok ABCD.EFGH

Unsur-unsur Balok

1. TITIK SUDUT :  

     

Titik sudut pada balok adalah titik temu / titik potong ketiga rusuk (titik pojok balok).

Pada balok ABCD.EFGH terdapat 8 buah titik sudut yaitu :

2. RUSUK BALOK :

Rusuk balok merupakan garis potong antara sisi-sisi balok.
Penulisan / penamannya rusuk menggunakan notasi dua huruf kapital.
Pada balok ABCD.EFGH terdapat 12 rusuk yang sama panjang yaitu :

Rusuk Alas : AB, BC, CD, AD
Rusuk Tegak : AE, BF, CG, DH
Rusuk Atas :  EF, FG, GH, EH

   

3. BIDANG / SISI BALOK

                

    Balok dibatasi oleh 6 buah bidang / sisi berbentuk persegipanjang, sisi-sisi yang berhadapan     sejajar dan kongruen.

    Penyebutan / penamaan sisi balok dengan menggunakan notasi empat huruf kapital secara siklis     atau melingkar.

    Bidang / sisi balok adalah :

1. Sisi alas         = ABCD
2. Sisi atas        = EFGH
3. Sisi depan     = ABFE
4. Sisi belakang = CDHG
5. Sisi kiri         = ADHE
6. Sisi kanan     = BCGF

    Sisi ABCD = EFGH , sisi ABFE = CDHG , sisi ADHE = BCGF

4. DIAGONAL SISI / BIDANG

    Diagonal sisi / bidang suatu balok adalah ruas garis yang menghubungkan dua titik sudut     berhadapan pada sebuah sisi. Terdapat 12 buah diagonal sisi balok.

    

    Panjang diagonal sisi AC = BD = EG = HF 
    Panjang diagonal sisi AF = BE = CH = DG 
    Panjang diagonal sisi AH = DE = BG = CF

5. DIAGONAL

Diagonal ruang sebuah balok adalah ruas garis yang menghubungkan dua titik sudutberhadapan dalam balok. Diagonal ruang balok saling berpotongan di tengah-tengah dan membagi dua diagonal ruang sama panjang.

    Panjang diagonal ruang AG = BH = CE = AF
    Terdapat 4 buah diagonal ruang pada sebuah kubus dengan panjang sama.

6. BIDANG DIAGONAL

    Bidang diagonal balok adalah bidang yang melalui dua buah rusuk yang berhadapan.
    Bidang diagonal balok membagi balok menjadi dua bagian yang sama besar.
    Terdapat 6 buah bidang diagonal, yaitu : ACGE, BDHF, ABGH, CDEF, ADGF, BCHE

    Bidang diagonal ACGE = BDHF, ABGH = CDEF, ADGF, BCHE

  

Jaring-jaring Balok

Sebuah balok apabila dipotong menurut rusuk-rusuknya kemudian tiap sisinya direntangkan akan membentuk jaring-jaring balok.

Enam buah persegipanjang  yang terdiri dari 3 pasang persegipanjang yang kongruen kalau disusun belum tentu merupakan jaring-jaring balok. Susunan persegipanjang tersebut merupakan jaring-jaring balok apabila dilipat kembali membentuk sebuah balok.

Luas Permukaan Balok

Perhatikan gambar balok !

Luas ABCD = AB x  BC = p x  l
Luas ABFE  = AB x  BF = p x  t
Luas ADHE = AD x  AE = l x  t
Luas Permukaan balok ABCD.EFGH = 2 Luas ABCD + 2 Luas ABFE + 2 Luas ADHE
                                                        = 2 pl + 2 pt + 2 lt

Volume Balok

Perhatikan balok ABCD.EFGH !

Luas Alas ABCD = AB x  BC
                          = p x  l
                          = pl

Volum balok = Luas Alas ABCD x  tinggi
                    = pl x  t

kubus

Definisi Kubus

Kubus adalah suatu bangun ruang yang dibatasi oleh enam buah sisi berbentuk persegi yang kongruen

Terdapat 6 buah sisi kongruen yang berbentuk persegi yang akan membatasi KUBUS, posisinya adalah:

  

Add caption

 1.    sisi alas

2.    sisi depan

3.    sisi atas

4.    sisi belakang

5.    sisi kiri

6.    sisi kanan

Penamaan kubus disesuaikan dengan sisi alas dan sisi atas.

Jika sisi alas kubus ABCD, dan sisi atas kubus EFGH, maka kubus tersebut dinamakan kubus ABCD.EFGH

Unsur-unsur Kubus

1. Titik Sudut

Titik sudut pada kubus adalah titik temu atau titik potong ketiga rusuk (titik pojok kubus).

Pada kubus ABCD.EFGH terdapat 8 buah titik sudut yaitu :
A, B,C,D, E, F, G, H, 

 2.Rusuk Kubus

Rusuk kubus merupakan garis potong antara sisi-sisi kubus. Penulisan atau penamaan rusuk menggunakan notasi dua huruf kapital.
Pada kubus ABCD.EFGH terdapat 12 rusuk yang sama panjang yaitu :
Rusuk Alas : AB, BC, CD, AD
Rusuk Tegak : AE, BF, CG, DH
Rusuk Atas :  EF, FG, GH, EH

3. Bidang / Sisi Kubus

                    

Bidang / sisi kubus adalah :

1.    Sisi alas = ABCD

2.    Sisi atas = EFGH

3.    Sisi depan = ABFE

4.    Sisi belakang = CDHG

5.    Sisi kiri = ADHE

6.    Sisi kanan = BCGF

Sisi / Bidang ABCD = EFGH = ABFE = CDHG = ADHE = BCGF

4. Diagonal Sisi / Bidang

Diagonal sisi / bidang adalah ruas garis yang menghubungkan dua titik sudut berhadapan pada sebuah sisi kubus.

Panjang diagonal sisi AC = BD = EG = HF = AF = BE = CH = DG = AH = DE = BG = CF

 

Panjang diagonal sisi AC = BD = EG = HF = AF = BE = CH = DG = AH = DE = BG = CF

5. Diagonal Ruang

Diagonal ruang sebuah kubus adalah ruas garis yang menghubungkan dua titik sudut berhadapan dalam kubus. Diagonal ruang kubus berpotongan di tengah-tengah kubus.

Panjang diagonal ruang AG = BH = CE = DF
Terdapat 4 buah diagonal ruang pada sebuah kubus dengan panjang sama.

6. Bidang Diagonal

Bidang diagonal kubus adalah bidang yang memuat dua rusuk berhadapan dalam suatu kubus. Bidang diagonal kubus berbentuk persegi panjang.
Terdapat 6 buah bidang diagonal, yaitu : ACGE, BDHF, ABGH, CDEF, ADGF, BCHE
Bidang diagonal ACGE = BDHF = ABGH = CDEF = ADGF = BCHE

Jaring-jaring Kubus

Sebuah kubus apabila dipotong menurut rusuk-rusuknya kemudian tiap sisinya direntangkan akan menghasilkan jaring-jaring kubus.

Jaring-jaring kubus terdiri dari enam buah persegi kongruen yang saling berhubungan

1. Luas Permukaan Kubus

Kubus ABCD.EFGH dengan panjang rusuk s satuan

Luas BCGF   = s x s
                    = s²
Luas Permukaan Kubus ABCD.EFGH
                    = 6 x  Luas BCGF
                    = 6.s²
Luas Permukaan Kubus dengan panjang sisi s satuan adalah 6.s² satuan luas

2. Contoh Soal

1. Hitung Luas permukaan kubus dengan panjang rusuk 7 cm !

Jawab :
Luas permukaan kubus = 6 x s²
    = 6 x 72
    = 6 x 49
    = 294 cm²

2. Hitung Luas permukaan kubus jika luas salah satu sisinya 10 cm² !

Jawab :
Luas salah satu sisi   = 10
                           s² = 10
Luas permukaan kubus = 6 x s²
                                      = 6 x 10²
                                      = 6 x 100
                                      = 600 cm²

3. Luas permukaan kubus adalah 600 cm². Hitung panjang rusuk kubus tersebut !

Jawab :

Luas permukaan kubus = 6 x s²    600  = 6 x s²
       s² =  
     s²   = 100
     s     = 10 cm

Volum Kubus

1. Volum Kubus

Kubus ABCD dengan panjang rusuk s satuan

Luas Alas ABCD  = sisi x sisi
                             = s x  s
                             = s²
Volum Kubus       = Luas Alas ABCD x  tinggi
                          = s²                       x  s
                          = s³

Volum Kubus dengan panjang sisi s satuan adalah s3 satuan volum.

2. Contoh Soal

1. Hitung Volum kubus yang mempunyai rusuk 9 cm !

Jawab :

Volum   = s³
            = 9³
            = 729 cm³.

2. Hitung Volum kubus jika luas salah satu sisinya 9 cm² !

Jawab :

Luas salah satu sisi = 9
                         s² = 9
                         s  = 3 cm

Volum  = s³
           = 3³
           = 27 cm³

3. Volum sebuah kubus adalah 125 cm³. Hitung panjang rusuk kubus tersebut !

Jawab :

Volum = s³

125     = s³

5³       = s³
s         = 5 cm

L I M A S

Definisi Limas

Limas adalah suatu bangun ruang yang dibatasi oleh sebuah segi banyak (segi n) dan segitiga-segitiga yang mempunyai titik puncak persekutuan di luar bidang segibanyak itu.

Garis t disebut tinggi limas dan titik T disebut  titik puncak.

Seperti prisma, nama limas juga berdasarkan jumlah segi-n sisi alasnya. Apabila alas limas berupa segi-n beraturan dan tiap sisi tegak merupakan segitiga sama kaki yang beraturan, maka limasnya disebut limas segi-n beraturan.

Unsur-unsur Limas

Unsur- unsur  yang dimiliki oleh suatu limas :

1. Titik sudut 
2. Rusuk
3. Bidang sisi

Ciri-ciri suatu limas :

1. Bidang atas berupa sebuah titik ( lancip )
2. Bidang bawah berupa bangun datar
3. Bidang sisi tegak berupa segitiga.

Untuk memberi nama sebuah limas, lihat bidang alasnya

Contoh-contoh Limas :

1. Limas Segitiga T.ABC 

Pada gambar di samping menunjukkan limas segitiga yang mempunyai : 4 titik sudut  : A, B, C dan T 4 bidang sisi : ABC, ABT, BCT dan ACT 6 rusuk         : AB, BC, CA, AT, BT dan CT

2. Limas Segiempat T.ABCD Pada gambar di samping menunjukkan limas segiempat yang mempunyai : 5 titik sudut  : A, B, C, D dan T  5 bidang sisi : 1 sisi alas yaitu ABCD                        4 sisi tegak yaitu TAB, TBC, TCD dan TAD 8 rusuk         : 4 rusuk alas yaitu AB, BC, CD dan DA                        4 rusuk tegak yaitu AT, BT, CT dan DT

3. Limas Segilima T.ABCDE

Pada gambar di samping menunjukkan limas segilima yang mempunyai : 6 titik sudut  : A, B, C, D, E dan T  6 bidang sisi : 1 sisi alas yaitu ABCDE  5 sisi tegak yaitu TAB, TBC, TCD, TDE, TAE 10 rusuk yaitu : 5 rusuk alas yaitu AB, BC, CD, DE dan EA    5 rusuk tegak yaitu AT, BT, CT, DT dan ET

4. Limas Segienam T.ABCDEF

Pada gambar di samping menunjukkan limas segienam yang mempunyai : 7 titik sudut  : A, B, C, D, E, Fdan T  7 bidang sisi : 1 sisi alas yaitu ABCDEF                        6 sisi tegak yaitu TAB, TBC, TCD, TDE, TEF, TAF 12 rusuk       : 6 rusuk alas yaitu AB, BC, CD, DE, EF, AF                         6 rusuk tegak yaitu AT, BT, CT, DT, ET, FT

5. Limas Segi-n

    Limas segi-n mempunyai:

    

Jaring-jaring Limas

Jaring-jaring merupakan bentuk dua dimensi dari suatu bangun tiga dimensi. 
Jaring-jaring limas dapat dibentuk dengan memotong beberapa rusuk limas

Contoh jaring-jaring limas:

1. Limas segitiga T.ABC

Sebuah limas T.ABC apabila rusuk TA, TB dan TC dipotong maka akan membentuk bidang datar yang disebut jaring-jaring limas segitiga.

2. Limas segiempat T.ABCD

Sebuah limas T.ABCD apabila rusuk TA, TB, TC dan TD dipotong maka akan membentuk bidang     datar yang disebut jaring-jaring limas segiempat. 

Luas Permukaan Limas

Luas permukaan limas dapat ditentukan dengan menjumlahkan luas sisi-sisi tegak dan luas alas.
Misal : 
           limas segitiga T.ABC

      

Jika dipotong menurut rusuk-rusuk TC, TB dan TA, maka didapat jaring-jaring :

    

Luas permukaan limas  =  luasT.AB + luasT.AC + luas T.BC + L.ABC
                                     =  (luasT.AB + luasT.AC + luas T.BC) + L.ABC

                                     =  jumlah luas sisi tegak + luas alas

Kesimpulan :

               

Contoh :

Sebuah limas segi empat beraturan, rusuk-rusuk alasnya 15 cm dan jarak dari puncak ke rusuk alas 20 cm.  Tentukan luas sisi limas !

Jawab :

Volum Limas

Volum limas dapat ditentukan dengan membelah sebuah kubus bersisi r menjadi enam buah limas yang kongruen, dimana: 
                                      

Maka didapat :
                         

Kesimpulan :

                   

Contoh :

Hitunglah volum limas yang mempunyai tinggi 30 cm dan luas alas 100 cm2  !

Jawab :

            

 Prisma Sistem Persamaan Linear

SOLUSI DARI SISTEM PERSAMAAN Suatu sistem persamaan mengacu pada sejumlah persamaan dengan jumlah yang sama variabel. Kami hanya akan melihat kasus dua persamaan linear dalam dua variabel. Situasi akan jauh lebih kompleks karena meningkatnya jumlah tidak diketahui, dan sistem yang lebih besar biasanya menyerang dengan bantuan komputer. Sebuah sistem dua persamaan linear dalam dua variabel dapat terlihat seperti Ini adalah bentuk standar untuk menulis persamaan ketika mereka adalah bagian dari sistem persamaan: variabel pergi dalam rangka di sisi kiri dan suku konstanta adalah di sebelah kanan. Braket di sebelah kiri menunjukkan bahwa kedua persamaan ini dimaksudkan untuk diselesaikan secara bersamaan, tetapi tidak selalu digunakan. Ketika kita berbicara tentang solusi dari sistem persamaan, kita berarti nilai-nilai dari variabel yang membuat kedua persamaan benar pada saat yang sama. Mungkin ada banyak pasangan x dan yyang membuat persamaan pertama benar, dan banyak pasangan x dan y yang membuat persamaan kedua benar, tapi kita mencari x dan y yang akan bekerja di kedua persamaan. Pada halaman berikut kita akan melihat metode aljabar untuk mencari solusi ini, jika ada. Karena ini adalah persamaan linier, grafik mereka akan garis lurus. Hal ini dapat membantu kita memvisualisasikan situasi grafis. Ada tiga kemungkinan: 1. Independen Persamaan ·         Garis berpotongan ·         Salah satu solusi Dalam hal ini dua persamaan menggambarkan garis yang berpotongan pada satu titik tertentu. Jelas hal ini adalah pada kedua saluran, dan karena koordinat (x, y) akan memenuhi persamaan garis baik. Dengan demikian pasangan (x, y) adalah solusi satu-satunya untuk sistem persamaan. 2. Tergantung Persamaan ·         Persamaan menggambarkan jalur yang sama ·         Tak terbatas jumlah solusi Kadang-kadang dua persamaan mungkin tampak berbeda namun sebenarnya menggambarkan jalur yang sama. Misalnya, dalam Persamaan kedua hanya dua kali persamaan pertama, sehingga mereka benar-benar setara dan apakah keduanya persamaan garis yang sama. Karena kedua persamaan menggambarkan jalur yang sama, mereka memiliki semua poin mereka yang sama; maka terdapat jumlah tak terbatas solusi ke sistem. Mencoba untuk memecahkan memberikan identitas Jika Anda mencoba untuk menyelesaikan suatu sistem tergantung dengan metode aljabar, Anda akhirnya akan berjalan ke sebuah persamaan yang identitas. Identitas adalah persamaan yang selalu benar, tidak tergantung pada nilai (s) dari setiap variabel (s). Sebagai contoh, Anda mungkin mendapatkan persamaan yang terlihat seperti x = x, atau 3 = 3. Hal ini akan memberitahu Anda bahwa sistem adalah sistem tergantung, dan Anda bisa berhenti di sana karena Anda tidak akan menemukan solusi yang unik. 3. Persamaan tidak konsisten Garis tidak berpotongan (Garis Paralel, memiliki kemiringan yang sama) Tidak ada solusi Jika dua baris kebetulan memiliki kemiringan yang sama, tetapi tidak identik baris yang sama, maka mereka tidak akan pernah berpotongan. Tidak ada pasangan (x, y) yang dapat memenuhi kedua persamaan, karena tidak ada titik (x, y) yang secara bersamaan pada kedua saluran. Dengan demikian persamaan ini dikatakan tidak konsisten, dan tidak ada solusi.Fakta bahwa mereka berdua memiliki kemiringan yang sama mungkin tidak jelas dari persamaan, karena mereka tidak ditulis dalam salah satu bentuk standar untuk garis lurus. Kemiringan tidak mudah terlihat dalam bentuk yang kita gunakan untuk menulis sistem persamaan. (Jika Anda berpikir tentang hal ini Anda akan melihat bahwa lereng adalah negatif dari koefisien darix dibagi dengan koefisien dari y). Mencoba untuk memecahkan memberikan pernyataan palsu Dengan mencoba untuk memecahkan suatu sistem persamaan aljabar, Anda beroperasi pada palsu asumsi-yaitu bahwa solusi ada. Hal ini pada akhirnya akan membawa Anda ke sebuahkontradiksi: pernyataan yang jelas palsu, terlepas dari nilai (s) dari variabel (s). Pada titik tertentu dalam pekerjaan Anda, Anda akan mendapatkan persamaan jelas palsu seperti 3 = 4.Hal ini akan memberitahu Anda bahwa sistem persamaan tidak konsisten, dan tidak ada solusi.  Solusi oleh Graphing Untuk sistem yang lebih kompleks, dan terutama yang mengandung non-linear persamaan, menemukan solusi dengan metode aljabar bisa sangat sulit atau bahkan mustahil.Menggunakan kalkulator grafik (atau komputer), Anda dapat grafik persamaan dan benar-benar melihat di mana mereka berpotongan. Kalkulator kemudian dapat memberikan koordinat titik persimpangan. Satu-satunya kekurangan metode ini adalah bahwa solusi ini hanya perkiraan, sedangkan metode aljabar memberikan solusi yang tepat. Dalam situasi yang paling praktis, meskipun, ketepatan kalkulator sudah cukup.Untuk aplikasi ilmiah dan rekayasa lebih menuntut ada komputer metode yang dapat menemukan perkiraan solusi untuk presisi sangat tinggi.

PENAMBAHAN METODE Seluruh masalah dengan memecahkan sistem persamaan adalah bahwa Anda tidak dapat memecahkan persamaan yang memiliki dua variabel di dalamnya. Anda membutuhkan persamaan dengan satu variabel sehingga Anda dapat memisahkan variabel yang di satu sisi dari persamaan. Kedua metode yang kita akan melihat beberapa teknik untuk menghilangkan salah satu variabel untuk memberikan persamaan hanya dalam satu yang tidak diketahui, yang kemudian dapat diselesaikan dengan metode biasa. Metode pertama untuk memecahkan sistem persamaan linier adalah metode Selain itu, di mana dua persamaan ditambahkan bersama-sama untuk menghilangkan salah satu variabel. Menambahkan persamaan berarti bahwa kita menambahkan sisi kiri dari dua persamaan bersama, dan kita menambahkan sisi kanan bersama-sama. Ini adalah hukum karena Prinsip Penambahan, yang mengatakan bahwa kita dapat menambahkan jumlah yang sama untuk kedua sisi persamaan. Karena sisi kiri dan kanan persamaan apapun adalah sama satu sama lain, kita memang menambahkan jumlah yang sama untuk kedua sisi persamaan. Pertimbangkan contoh sederhana ini: Contoh: Jika kita menambahkan persamaan ini bersama-sama, istilah yang mengandung y akan menambahkan hingga nol (2 y ditambah - 2 y), dan kami akan atau 5 x = 5  x = 1 Namun, kami belum selesai-kita tahu x, tapi kami masih belum tahu y. Kita dapat memecahkan untuk y dengan menggantikan nilai sekarang dikenal untuk x menjadi baik persamaan asli kami. Ini akan menghasilkan persamaan yang dapat diselesaikan untuk y: Sekarang kita tahu kedua x dan y, kita dapat mengatakan bahwa solusi untuk sistem adalah pasangan (1, 1/2). Contoh terakhir adalah mudah untuk melihat karena kehadiran beruntung dari kedua positif dan y 2 negatif. Salah satunya adalah ini tidak selalu beruntung. Mempertimbangkan Contoh: Sekarang ada yang lebih jelas, tetapi masih ada sesuatu yang bisa kita lakukan. Jika kita kalikan persamaan pertama oleh - 3, kita mendapatkan (Jangan lupa untuk berkembang biak setiap istilah dalam persamaan, di kedua sisi tanda sama dengan). Sekarang jika kita menambahkan mereka bersama-sama istilah yang mengandung x akan membatalkan: atau Seperti dalam contoh sebelumnya, sekarang kita tahu y ​​kita dapat menyelesaikan untuk x dengan menggantikan menjadi baik persamaan asli. Persamaan pertama tampak seperti termudah untuk menyelesaikan untuk x, jadi kita akan menggunakannya: Dan sehingga titik solusinya adalah (- 4, 7/2). Sekarang kita lihat contoh bahkan kurang jelas: Contoh: Di sini tidak ada yang sangat menarik tentang mengejar baik x atau y. Dalam kedua kasus, kedua persamaan harus dikalikan oleh beberapa faktor untuk sampai pada koefisien umum. Ini sangat mirip situasi yang Anda hadapi berusaha mencari denominator paling umum untuk menambahkan pecahan, kecuali bahwa di sini kita menyebutnya Beberapa Terkecil Umum (LCM). Sebagai aturan umum, paling mudah untuk menghilangkan variabel dengan LCM terkecil. Dalam hal ini yang akan menjadi y, karena LCM dari 2 dan 3 adalah 6. Jika kita ingin menghilangkan x kita harus menggunakan LCM dari 10 (5 kali 2). Jadi, kita memilih untuk membuat koefisien dari y ke plus dan minus 6. Untuk melakukan ini, persamaan pertama harus dikalikan dengan 3, dan persamaan kedua oleh 2: atau Sekarang menambahkan kedua bersama-sama akan menghilangkan hal yang mengandung y: atau x = 2 Kami masih harus mengganti nilai ini menjadi satu dari persamaan asli untuk memecahkan y: Jadi solusinya adalah titik (2, 2).

PERGANTIAN CARA Ketika kita menggunakan Metode Penambahan untuk memecahkan sistem persamaan, kita masih harus melakukan substitusi untuk memecahkan untuk variabel yang tersisa. Dengan metode substitusi, kita memecahkan salah satu persamaan untuk satu variabel dalam hal lain, dan kemudian menggantikan itu ke persamaan lainnya. Ini lebih masuk akal dengan contoh: Contoh: 2 y + x = 3 (1) 4 y - ​​3 x = 1 (2) Persamaan 1 tampak seperti itu akan mudah untuk menyelesaikan untuk x, jadi kami bawa dan mengisolasi x: 2 y + x = 3 x = 3 - 2 y (3) Sekarang kita dapat menggunakan hasil ini dan pemain pengganti 3 - 2 untuk x y di dalam persamaan 2: Sekarang kita memiliki y, kita masih perlu untuk mengganti kembali untuk mendapatkan x. Kita bisa mengganti kembali ke salah satu persamaan sebelumnya, tetapi melihat bahwa persamaan 3 adalah sudah mudah diselesaikan untuk x: Maka solusinya adalah (1, 1). Sebagai aturan, metode substitusi lebih mudah dan lebih cepat daripada metode Selain itu ketika salah satu persamaan ini sangat sederhana dan mudah dapat diselesaikan untuk salah satu variabel. Graping Dan Garis Lurus RECTANGULAR KOORDINAT Sistem koordinat persegi panjang juga dikenal sebagai sistem koordinat Cartesian setelah Rene Descartes, yang dipopulerkan penggunaannya dalam geometri analitik. Sistem koordinat persegi panjang didasarkan pada kotak, dan setiap titik di pesawat dapat diidentifikasi dengan x dan y koordinat yang unik, seperti setiap titik di Bumi dapat diidentifikasi dengan memberikan lintang dan bujur. Axes Lokasi di grid diukur relatif terhadap titik tetap, yang disebut asal, dan diukur sesuai dengan jarak sepanjang sepasang sumbu. Sumbu x dan y hanya seperti garis bilangan, dengan jarak positif untuk jarak yang benar dan negatif di sebelah kiri dalam kasus sumbu x, dan diukur positif dan negatif ke atas ke bawah untuk sumbu y. Setiap perpindahan dari asal dapat dibangun dengan memindahkan jarak tertentu dalam arah x dan kemudian lagi jarak dalam arah y. Anggap saja sebagai jika Anda memberikan petunjuk kepada seseorang dengan mengatakan sesuatu seperti "pergi tiga blok Timur dan kemudian 2 blok Utara." Koordinat , Graphing Poin Kami menentukan lokasi sebuah titik dengan terlebih dahulu memberikan yang koordinat x (perpindahan kiri atau kanan dari titik asal), dan kemudian koordinat y (atas atau bawah perpindahan dari asal). Dengan demikian, setiap titik di pesawat dapat diidentifikasi oleh sepasang angka (x, y), yang disebut koordinat. Contoh: Kuadran Terkadang kita hanya ingin tahu apa bagian umum dari grafik yang kita bicarakan. Sumbu alami membagi pesawat menjadi perempat. Kami menyebutnya kuadran, dan jumlah mereka dari satu sampai empat. Perhatikan bahwa penomoran dimulai di kuadran kanan atas dan terus berputar ke arah berlawanan arah jarum jam. Perhatikan juga bahwa masing-masing kuadran dapat diidentifikasi dengan kombinasi unik dari tanda-tanda positif dan negatif untuk koordinat titik pada kuadran itu. GRAFIK FUNGSI Pertimbangkan persamaan seperti y = 2 x - 1 Kita katakan bahwa y adalah fungsi dari x karena jika Anda memilih nilai untuk x, formula ini akan memberikan nilai unik dari y. Sebagai contoh, jika kita pilih x = 3 maka rumus memberi kita y = 2 (3) - 1 atau y = 5 Demikian kita dapat mengatakan bahwa nilai y = 5 dihasilkan oleh pilihan dari x = 3. Seandainya kita memilih nilai yang berbeda untuk x, kita akan mendapatkan nilai yang berbeda untuk y.Bahkan, kita bisa memilih sejumlah besar nilai yang berbeda untuk x dan mendapatkan nilai y untuk masing-masing. Hal ini paling terlihat pada tabel: x (Input) x → FORMULA → y y (Output) -2 2 (-2) - 1 = -5 -5 -1 2 (-1) - 1 = -3 -3 0 2 (0) - 1 = -1 -1 1 2 (1) - 1 = 1 1 2 2 (2) - 1 = 3 3 3 2 (3) - 1 = 5 5 Hubungan antara x dan nilai y yang sesuai menghasilkan koleksi pasang titik (x, y), yaitu (-2, -5) (-1, -3) (0, -1) (1, 1) (2, 3) (3, 5) Karena masing-masing pasang nomor bisa koordinat titik di pesawat, adalah wajar untuk bertanya apa koleksi pasangan terurut akan terlihat seperti jika kita digambarkan mereka. Hasilnya adalah seperti ini: Poin yang tampaknya jatuh dalam garis lurus. Sekarang, pilihan kita untuk x cukup sewenang-wenang. Kita bisa juga telah memilih nilai-nilai lain, termasuk non-integer nilai. Misalkan kita mengambil banyak nilai lebih untuk x, seperti 2,7, dll 3,14 dan menambahkan mereka ke grafik kita. Akhirnya poin akan begitu ramai bersama bahwa mereka akan membentuk garis utuh: Panah pada ujung baris menunjukkan bahwa ia pergi selamanya, karena tidak ada batas untuk apa nomor kita bisa memilih untuk x. Kami mengatakan bahwa baris ini adalah grafik dari fungsi y = 2 x - 1. Jika Anda memilih setiap titik pada baris ini dan membacakan x dan koordinat y, mereka akan memenuhi persamaan y = 2 x - 1. Misalnya, titik (1,5, 2) adalah pada baris: dan koordinat x = 1,5, y = 2 memenuhi persamaan y = 2 x - 1: 2 = 2 (1,5) - 1 ·         Catatan: Grafik ini ternyata menjadi garis lurus hanya karena fungsi tertentu yang kita gunakan sebagai contoh. Ada banyak fungsi lainnya yang grafik berubah menjadi kurva berbagai. GARIS LURUS Persamaan Linear Dua Variabel dalam Persamaan y = 2 x - 1 yang kita gunakan sebagai contoh untuk fungsi grafik yang dihasilkan grafik yang merupakan garis lurus. Ini bukanlah kebetulan. Persamaan ini adalah salah satu contoh dari kelas umum dari persamaan yang kita sebut persamaan linear dalam dua variabel. Dua variabel biasanya (tapi tentu saja tidak harus) x dan y. Persamaan ini disebut linear karena grafik mereka berupa garis lurus. Persamaan linear yang mudah untuk mengenali karena mereka mematuhi aturan berikut: Variabel (biasanya x dan y) muncul hanya untuk listrik pertama Variabel dapat dikalikan hanya dengan konstanta bilangan real Setiap istilah bilangan real dapat ditambahkan (atau dikurangkan, tentu saja) Tidak ada lagi yang diperbolehkan! Ini berarti bahwa setiap persamaan yang mengandung hal-hal seperti x 2, y 2, 1 / x, xy, akar kuadrat, atau fungsi lain dari x atau y adalah tidak linier. Menggambarkan Garis Seperti halnya ada jumlah tak terbatas persamaan yang memenuhi kondisi di atas, ada juga jumlah tak terbatas garis lurus yang kita bisa menggambar grafik. Untuk menggambarkan garis tertentu kita harus menetapkan dua bagian yang berbeda dari informasi mengenai garis itu. Sebuah garis lurus tertentu dapat ditentukan dengan menentukan dua titik yang berbeda yang melewati garis, atau dapat ditentukan dengan memberikan satu titik yang melewati dan entah bagaimana menggambarkan bagaimana "miring" adalah baris. Lereng Kemiringan garis adalah ukuran seberapa "miring" adalah baris. Sebuah tanda jalan raya mungkin mengatakan sesuatu seperti "kelas 6% di depan." Apa artinya ini, selain itu Anda berharap karya rem Anda? Artinya adalah bahwa rasio drop di ketinggian untuk jarak horizontal anda adalah 6%, atau 6/100. Dengan kata lain, jika Anda memindahkan 100 meter ke depan, Anda akan turun 6 kaki, jika Anda bergerak 200 meter ke depan, Anda akan turun 12 kaki, dan sebagainya. Kami mengukur kemiringan garis dalam banyak cara yang sama, meskipun kita tidak mengubah hasilnya ke persen. Misalkan kita memiliki grafik garis lurus yang tidak diketahui. Pilih dua titik yang berbeda pada baris dan label mereka menunjuk 1 dan titik 2: Dalam bergerak dari titik 1 ke titik 2, kita menutupi 4 langkah horizontal (arah x) dan 2 langkah vertikal (arah y): Oleh karena itu, rasio dari perubahan ketinggian dengan perubahan jarak horizontal adalah 2 sampai 4. Mengekspresikan sebagai suatu bagian dan mengurangi, kita mengatakan bahwa kemiringan garis ini adalah Untuk memformalkan prosedur ini sedikit, kita perlu berpikir tentang dua titik dalam x dan koordinat y. Sekarang Anda harus dapat melihat bahwa perpindahan horisontal adalah perbedaan antara koordinat x dari dua titik, atau 4 = 5 - 1, dan perpindahan vertikal adalah perbedaan antara koordinat y, atau 2 = 4 - 2. Secara umum, jika kita mengatakan bahwa koordinat titik 1 adalah (x 1, y 1) dan koordinat titik 2 adalah (x 2, y 2), maka kita dapat menentukan kemiringan m sebagai berikut: dimana (x 1, y 1) dan (x 2, y 2) adalah dua titik yang berbeda di telepon. Ini adalah adat (di AS) untuk menggunakan huruf m untuk mewakili lereng. Tidak ada yang tahu mengapa. Tidak ada bedanya mana dua poin digunakan untuk titik 1 dan titik 2. Jika mereka dialihkan, baik pembilang dan penyebut dari pecahan itu akan berubah menjadi tanda sebaliknya, memberikan hasil yang sama persis. Banyak orang merasa berguna untuk mengingat rumus ini sebagai "lereng adalah kenaikan lebih panjang." Notasi lain yang umum adalah  , Di mana huruf Yunani delta (D) berarti "perubahan masuk" Kemiringan adalah rasio berapa banyak perubahan y per perubahan x: Garis Horizontal Sebuah garis horizontal memiliki kemiringan nol, karena tidak ada perubahan dalam y dengan meningkatnya x. Dengan demikian, dua titik akan memiliki koordinat y yang sama, dan karenay 1 = y 2,  . Vertikal Sebuah garis vertikal menyajikan masalah yang berbeda. Jika Anda melihat rumus  , Anda melihat bahwa ada masalah dengan penyebut. Hal ini tidak mungkin untuk mendapatkan dua nilai yang berbeda untuk x l dan x 2, karena jika x berubah maka Anda tidak berada pada garis vertikal lagi. Dua titik pada garis vertikal akan memiliki koordinat x yang sama, dan x 2 - x 1 = 0. Karena penyebut dari pecahan tidak boleh nol, kita harus mengatakan bahwagaris vertikal memiliki kemiringan terdefinisi. Jangan bingung ini dengan kasus garis horizontal, yang memiliki kemiringan yang jelas yang kebetulan sama dengan nol. Positif dan Negatif Lereng Koordinat x meningkatkan ke kanan, sehingga bergerak dari kiri ke kanan adalah gerak dalam arah x positif. Misalkan Anda akan menanjak saat Anda bergerak dalam arah x positif.Kemudian kedua x dan koordinat y meningkat, sehingga rasio kenaikan selama jangka akan positif-Anda akan memiliki peningkatan positif dalam y untuk peningkatan positif dalam x. Di sisi lain, jika Anda akan menurun ketika kita bergerak dari kiri ke kanan, maka rasio kenaikan selama jangka akan negatif karena Anda kehilangan ketinggian untuk peningkatan positif diberikan dalam x. Hal yang perlu diingat adalah: Ketika Anda pergi dari kiri ke kanan, Uphill Lereng = Positif Downhill Lereng = Negatif Dan tentu saja, tidak ada perubahan dalam tinggi berarti bahwa garis memiliki kemiringan nol. Beberapa Lereng Penyadapan Dua garis dapat memiliki kemiringan yang sama dan berada di tempat yang berbeda pada grafik. Ini berarti bahwa selain menggambarkan kemiringan garis kita perlu beberapa cara untuk menentukan persis di mana garis tersebut pada grafik. Ini bisa dicapai dengan menetapkan satu titik tertentu yang melapisi melewati. Meskipun titik apapun akan dilakukan, ia konvensional untuk menentukan titik di mana garis melintasi sumbu y. Titik ini disebut y-intercept, dan biasanya dilambangkan dengan huruf b. Perhatikan bahwa setiap baris kecuali garis vertikal akan menyeberangi sumbu y di beberapa titik, dan kita harus menangani garis vertikal sebagai kasus khusus pula karena kita tidak dapat menentukan lereng untuk mereka. Sama Lereng, berbeda y penyadapan Persamaan Persamaan garis memberikan hubungan matematis antara koordinat x dan y dari suatu titik di telepon. Mari kita kembali ke contoh kita digunakan dalam grafik fungsi. Persamaan y = 2 x - 1 menghasilkan grafik berikut: Baris ini ternyata memiliki kemiringan 2 dan intersep y sama dengan -1. Nomor 2 dan -1 juga muncul dalam persamaan-koefisien dari x adalah 2, dan konstanta aditif adalah -1. Ini bukan kebetulan, tetapi karena bentuk standar di mana persamaan ini ditulis. Standar Formulir (Slope-Intercept Form) Jika suatu persamaan linear dalam dua variabel ditulis dalam bentuk y = mx + b di mana m dan b adalah setiap dua bilangan real, maka grafik akan menjadi garis lurus dengan kemiringan m dan intercept y sama dengan b. Point-Lereng Formulir Seperti disebutkan sebelumnya, garis sepenuhnya dijelaskan dengan memberikan lereng dan satu titik yang berbeda yang melewati garis. Sementara saat ini adalah lazim mencegat y, tidak perlu.Jika Anda ingin menggambarkan sebuah garis dengan kemiringan m diberikan yang melewati suatu titik (x 1, y 1), rumus ini Untuk membantu mengingat rumus ini, memikirkan pemecahan untuk m: Karena titik (x, y) adalah titik sembarang pada garis dan titik (x 1, y 1) adalah titik lain di telepon, ini tidak lebih dari definisi lereng untuk jalur itu. Dua-Point Formulir Cara lain untuk sepenuhnya menentukan garis adalah memberikan dua titik yang berbeda yang melewati garis. Jika anda diberikan garis melewati titik (x 1, y 1) dan (x 2, y 2), rumusnya adalah Formula ini juga mudah untuk diingat jika Anda melihat bahwa itu sama saja dengan bentuk titik-lereng dengan kemiringan m diganti dengan definisi lereng,